Research 遥感

DDPM笔记

更新时间

0. 参考文献

1. 常见生成模型

img

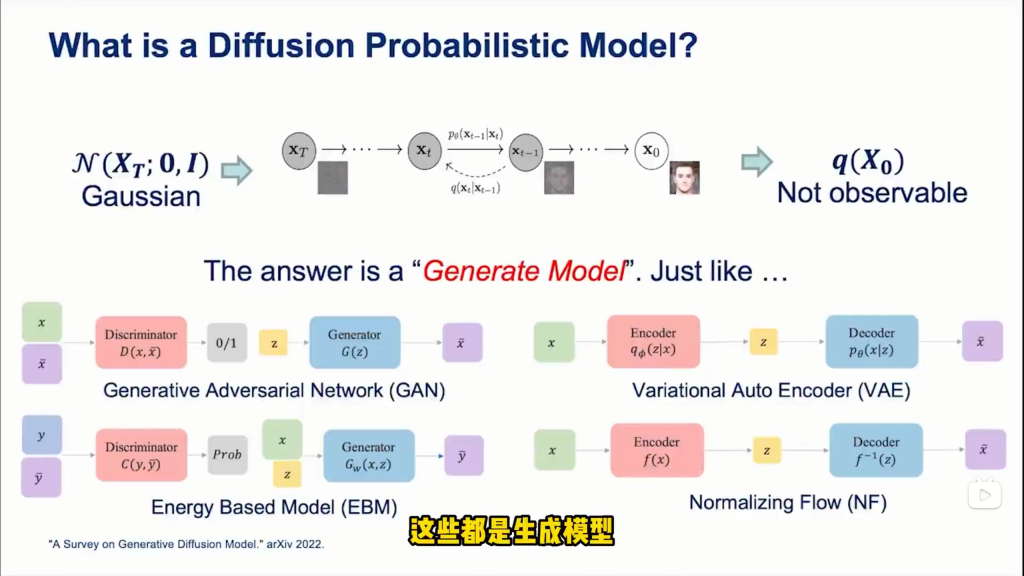
1.1 DDPM

工作原理

  • 扩散模型通过定义一个前向过程，将数据逐步添加噪声直至变为纯噪声。
  • 然后学习一个反向过程，从纯噪声开始逐步去噪还原数据。
  • 反向过程通常由神经网络参数化，通过最大化数据在每一步去噪时的对数似然来进行训练。

特点

  • 生成过程较慢，因为需要通过多个步骤逐步去噪。
  • 生成的样本质量高，并且随着更多去噪步骤的引入，质量可以进一步提高。
  • 理论上可以直接计算样本的生成概率。

1.2 GAN（对抗生成网络）

工作原理

  • GAN由生成器和判别器组成，二者互相对抗。
  • 生成器从噪声中生成数据。
  • 判别器判断数据是真实的还是生成的。
  • 生成器的目标是骗过判别器，使其认为生成的数据是真实的，而判别器的目标是尽可能准确地区分真实数据和生成数据。
  • 训练过程中，生成器和判别器进行博弈，逐渐提高生成数据的质量。

特点

  • 生成的样本质量高，视觉效果好，尤其在图像生成任务中表现出色。
  • 训练过程不稳定，容易出现模式崩溃（mode collapse）和梯度消失等问题。
  • 无法直接计算样本的生成概率。

1.3 VAE（变分自编码器）

工作原理

  • VAE由编码器和解码器组成。
  • 编码器将输入数据压缩到一个潜在空间，并输出一个潜在变量的分布（通常是高斯分布）。
  • 解码器从这个分布中采样，并将样本映射回原始数据空间。
  • VAE通过最小化重构误差和潜在分布与先验分布（通常是标准正态分布）之间的KL散度来进行训练。

特点

  • 理论基础扎实，能够明确地表示潜在空间。
  • 生成的样本通常质量较低，因为解码器输出的样本是从噪声中生成的。
  • 可以直接计算样本的生成概率。

1.4 EBM

略

1.5 NF

略

1.6 总结

  • VAE：适合需要明确表示潜在空间和计算生成概率的应用，但生成的样本质量相对较低。
  • GAN：适合需要高质量生成样本的应用，尤其是图像生成，但训练不稳定且无法计算生成概率。
  • 扩散模型（DDPM）：生成的样本质量高，生成过程较慢且稳定性较好，适合需要高质量生成样本的应用。

2. 讲解

文档讲解

What are Diffusion Models?

一文读懂扩散模型，DDPM原理+代码解读-CSDN博客

视频讲解

54、Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读哔哩哔哩bilibili

3. 数学基础

3.1 条件概率+BayesBayes公式

P(B | A)读作 P, B Given A

P(ABC) = P(C | BA) \cdot P(BA) = P(C | BA) \cdot P(B | A) \cdot P(A)

P(BC | A) = P(B | A) \cdot P(C | AB)（左右两边条件概率都展开即可）

3.2 马尔科夫链

假设有马尔科夫链A→B→CA→B→C

P(ABC) = P(C | BA) \cdot P(BA) = P(C | B) \cdot P(B | A) \cdot P(A)

P(BC | A) = P(B | A) \cdot P(C | B)

3.3 Jensen不等式

若f(x)是凸函数，则：

f(\sum_{i=1}^{n} \lambda_i x_i) \leq \sum_{i=1}^{n} \lambda_i f(x_i)

其中，∑_{i=1}^{n}λ_i=1。

如果为严格的凹函数，那么≤改为≥即可。

3.4 KL散度

两个单一变量的高斯分布p和q，

通过计算他们的KL散度可以计算出在近似一个分布与另一个分布时损失了多少信息，

从而更好地评估这两个不同概率分布之间的差异。

KL(p, q) = \log \frac{\sigma_2}{\sigma_1} + \frac{\sigma_1^2 + (\mu_1 – \mu_2)^2}{2 \sigma_2^2} – \frac{1}{2} \geq 0

3.5 参数重整化

若希望从高斯分布N(μ,σ)中采样，可以先从标准分布N(0,1)中采样出z，再得到μ+z∗σ。

这样做的好处是将随机性转移到z这个常量上，而μ和σ则当作仿射网络变换的一部分。

  • 允许梯度回传：在传统的随机采样过程中，随机性会阻断梯度回传。通过重参数化，模型可以将随机性外部化，从而允许梯度通过这些变量流向模型参数。
  • 降低方差：在训练过程中，由于噪声是独立采样的，重参数化有助于减少梯度估计的方差，从而提高训练的稳定性和效率。
  • 模型的可逆性：在扩散模型中，生成过程的关键在于可逆性。重参数化确保在给定噪声序列的情况下，可以从噪声状态逆向恢复出干净的数据。这种可逆性是通过训练网络来预测每一步的噪声而实现的，而不是直接预测下一步的数据状态。

因此，重参数化技巧在扩散模型中是一个强大的工具，它允许模型在保持生成过程随机性的同时，能够进行有效的训练。这是为什么扩散模型能够使用基于梯度的优化方法来学习生成数据的过程。

4. 数学推导

4.1 前向扩散过程

  1. 给定初始数据分布x_0∼q(x)，可以不断地向分布中添加高斯噪声，该噪声的标准差是以固定值β（很小的一个数，随着t增大而增大）而确定的，均值是以固定值$αt(α_t=1–β_t)和当前t时刻的数据x_t决定的。这个过程是一个马尔科夫链过程。
    即：    x_t = \sqrt{\alpha_t}x    {t-1}+\sqrt{1-\alpha_t}z_{t-1}$
  2. 随着t的不断增大，最终数据分布x变成了一个各向独立的高斯分布。

– q(x_t | x_{t-1}) = N(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I)
– \bar{\alpha_t}=\prod_{i=1}^{t}\alpha_i（其中\bar{\alpha_t}=\prod_{i=1}^{t}\alpha_i）
– q(x_{1:T} | x_0) = \prod_{t=1}^{T} q(x_t | x_{t-1})（联合概率分布）
3. 任意时刻的q(x_t)推导也可以完全基于x_0和β_t来计算出来，而不需要做迭代。 注意这里，两个独立的正态分布X \sim N(\mu_1, \sigma_1)和注意这里，两个独立的正态分布X \sim N(\mu_1, \sigma_1)和Y \sim N(\mu_2, \sigma_2)的叠加后的分布aX+bY的均值为a\mu_1 + b\mu_2，方差为a^2\sigma_1^2 + b^2\sigma_2^2。

4.2 逆扩散过程

逆扩散过程是从高斯分布中恢复原始数据，我们可以假设它也是一个高斯分布，但是无法逐步的拟合分布，所以需要构建一个参数分布来做估计。逆扩散过程仍然是一个马尔科夫链过程。

  • $p$为逆向扩散的概率分布，含变参
  • $q$为前向扩散的后验概率分布
  • DDPM使用神经网络p_\theta(x_{t-1} | x_t)拟合逆向过程q(x_{t-1} | x_t)

  • $p_\theta(x_{0:T}) = p(x_T)\prod_{t=1}^{T}p_\theta(x_{t-1} | x_t)$

  • $p_\theta(x_{t-1} | x_t) = N(x_{t-1};\mu_\theta(x_t, t), \sigma_\theta(x_t, t))$ —————————-(0)

  • $q(x_{t-1}|x_t, x_0) = N(x_{t-1}; \tilde{\mu}(x_t, x_0), \tilde{\beta_t}I)$ ——————————–(1)

（0）式和（1）式某种意义上来说是等价的。

注意：高斯分布的概率密度函数是f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} ———————————(2)

注意：ax^2+bx=a\left(x+\frac{b}{2a}\right)^2+C —————————————————(3)

后验的扩散条件概率q(x_{t-1}|x_t, x_0)分布是可以用贝叶斯公式推导出的，也就是说，给定x_t和x_0，可以计算出x_{t-1}，

即：q(x_{t-1}|x_t, x_0) = q(x_{t-1},x_t,x_0)

\propto exp\left(-\frac{1}{2}\left(\frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{\beta_t} + \frac{(x_{t-1}-\sqrt{\bar{\alpha_{t-1}}}x_0)^2}{1-\bar{\alpha_{t-1}}} – \frac{(x_{t}-\sqrt{\bar{\alpha_{t}}}x_0)^2}{1-\bar{\alpha_{t}}}\right)\right)

=exp\left( -\frac{1}{2} \left( (\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha_{t-1}}})x_{t-1}^2 – (\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar{\alpha_t}}}{1-\bar{\alpha_t}}x_0)x_{t-1} + C(x_t, x_0) \right) \right) ————————————(4)

结合（1）（2）（3）（4）式，可得：

  • $\tilde{\beta_t}=\frac{1-\bar{\alpha_{t-1}}}{1-\bar{\alpha_t}} \cdot \beta_t$

  • $\tilde{\mu_t}(x_t, x_0) = \frac{\sqrt{\alpha_t} (1-\bar{\alpha_{t-1}} )}{1 – \bar{\alpha_t}}x_t + \frac{\sqrt{\bar{\alpha_{t-1}}}\beta_t}{1-\bar{\alpha_t}}x_0$ ——————————————(5)

基于前向扩散过程（虽然并没有真的做了前向扩散）中x_t与x_0的关系，我们可以知道，

  • $x_0=\frac{1}{\sqrt{\bar{\alpha_t}}}(x_t-\sqrt{1-\bar{\alpha_t}}z_t)$ ————————————————————–(6)

将x_0的表达式代入（5）式中，可以重新给出该分布的均值表达式，也就是说，在给定x_0的条件下，后验条件高斯分布的均值计算只与x_t和z_t有关。

z_t是t时刻的随机正态分布变量，源自参数重整化。

  • $\tilde{\mu_t}=\frac{1}{\sqrt{\alpha_t}}(x_t – \frac{\beta_t}{\sqrt{1 – \bar{\alpha_t}}}z_t)$

重点来了：只有这个z_t(x_t, t; \theta)是需要用网络去拟合的

目标数据分布的似然函数

img

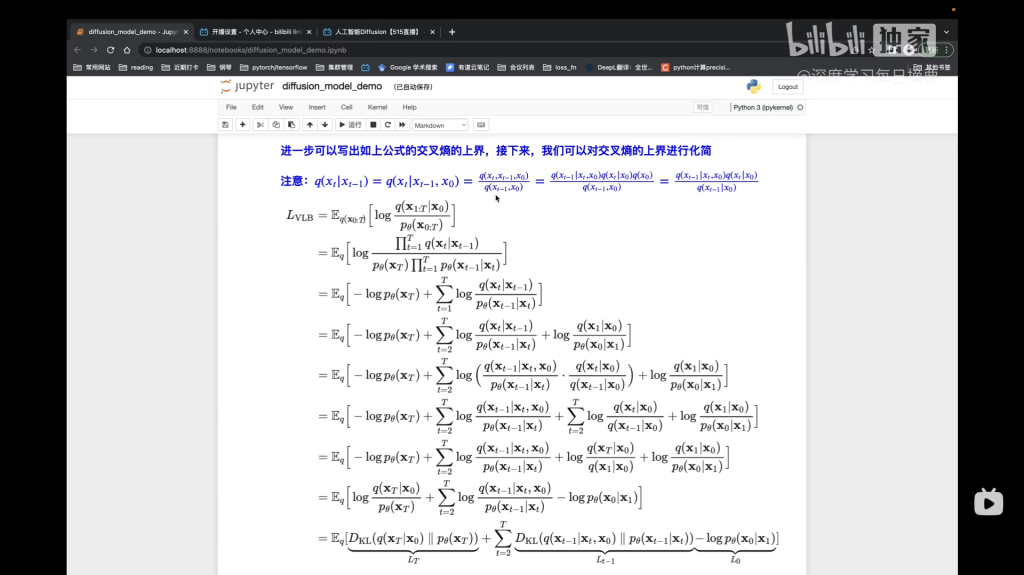
这里论文将p_\theta(x_{t-1}|x_t)分布的方差设置成一个与\beta相关的常数，因此可训练的参数只存在于其均值中。

5. 网络模块

5.1 Unet职责

无论在前向过程还是反向过程，Unet的职责都是根据当前的样本和时间t预测噪声，也就是Unet实现z_\theta(x_t, t)的预测，整个训练过程其实就是在训练Unet网络的参数。

5.2 Gaussion Diffusion职责

前向过程：从1到T的时间采样一个时间t，生成一个随机噪声加到图片上，从Unet获取预测噪声，计算损失后更新Unet梯度

反向过程：先从正态分布随机采样和训练样本一样大小的纯噪声图片，从T-1到0逐步重复以下步骤：从x_t还原x_{t-1}。

6. 训练过程

img

Algorithm1：Training

  • 从数据中抽取一个样本；

  • 从1-T中随机选取一个时间t；

  • 将x_0和t传给GD，GD采样一个随机噪声，加到x_0，形成x_t，然后将x_t和t放入Unet，Unet根据t生成正弦位置编码并和x_t结合，预测并返回加的这个噪声，GD再计算该噪声和随机噪声的损失；

  • 将神经网络Unet预测的噪声与之前GD采样的随机噪声求L2损失，计算梯度，更新权重；

  • 重复以上步骤，直到网络Unet训练完成。

Algorithm2：Sampling

  • 从标准正态分布采样出x_T

  • 从T, T−1, …. , 2, 1依次重复以下步骤：

    • 从标准正态分布采样z，为重参数化做准备；

    • 根据模型预测出z_\theta(x_t, t)，得到样本noise的均值，结合x_t，prednoise和z，利用重参数化技巧，得到x_{t-1}；

  • 循环结束后返回x_0；